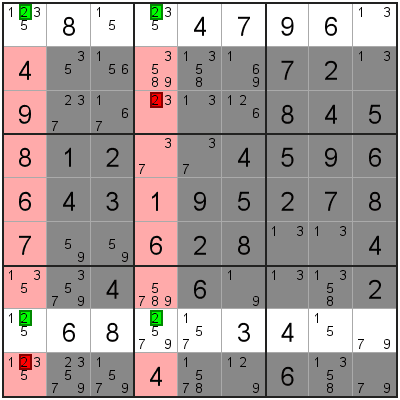
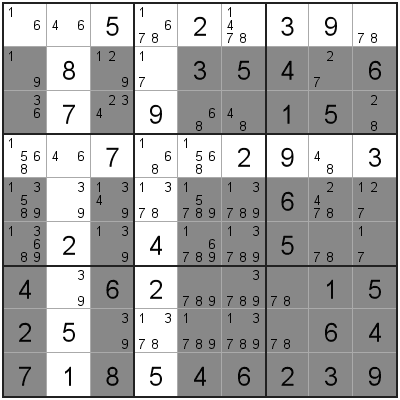
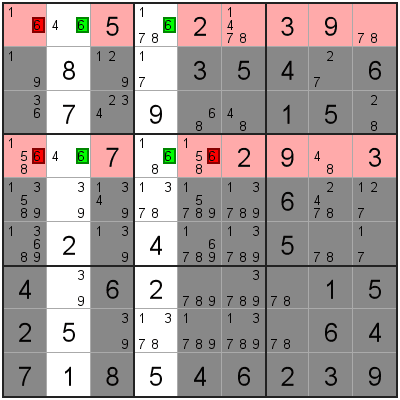
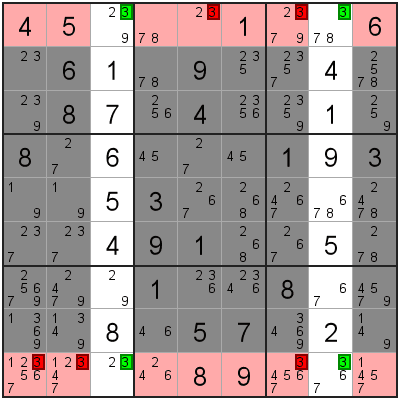
In this Sudoku grid we are looking at these 2 rows in particular.
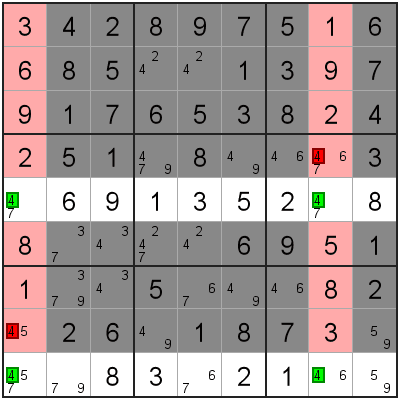
The 4 candidate appears exactly twice in these 2 rows.
They are also in the same two columns.
This means that there are only 2 possible ways the 4 value can appear in these two rows.
They can appear in this configuration.
Or, they can appear in this configuration.
No other configuration is possible.
Whichever configuration ends up being the solution, we know there can't be a 4 in any other cells in these 2 columns.
This means we can remove any 4 pencil marks from these 2 columns.
This is another example of a X-wing.
There is only two places the 6 candidate can appear in rows 1 and 3, and they are both in the same columns.
This means we can remove all other 6 candidates from these two columns.
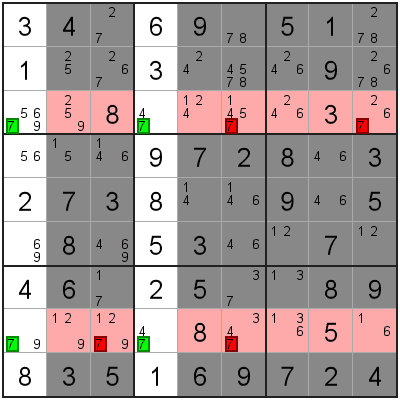
X-Wing can also appear in a row-configuration.
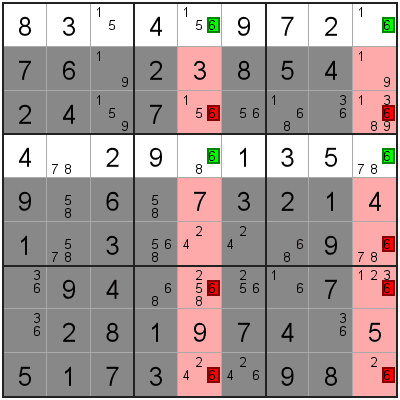
In this example, we have 2 columns where the 7 candidate appears exactly twice, and in the same row both times.
In exactly the same way, we can remove all other 7 candidates from these rows.
Another X-Wing in a row configuration where we can remove candidates from the rows.
Can you spot the X-Wing in this grid?
Did you spot it?
Can you spot the X-Wing in this grid?
Did you spot it?
Can you spot the X-Wing on the 3 candidates in this grid?
Did you spot it?
That's everything you need to know about X-Wing.
It's the first of the more advanced techniques that you need to know about.
When looking for X-Wing, you are looking for candidates that appear in exactly two rows and in the same column. Or, candidates that appear in exactly two columns and in the same row.
